Plain integers are at least 32 bits long. The range is at least -2,147,483,648 to 2,147,483,647 (approximately ±2 billion).

Python represents integers as strings of decimal digits. A number does not include any punctuation, and cannot begin with a leading zero (0). Leading zeros are used for base 8 and base 16 numbers. We'll look at this below.

>>> 
255+100

355
>>> 
397-42

355
>>> 
71*5

355
>>> 
355/113

3

While most features of Python correspond with common expectations from mathematics and other programming languages, the division operator, /, poses certain problems. Specifically, the distinction between the algorithm and the data representation need to be made explicit. Division can mean either exact floating-point results or integer results. Mathematicians have evolved a number of ways of describing precisely what they mean when discussing division. We need similar expressive power in Python.We'll look at more details of division operators in the section called “Division Operators”.

Octal and Hexadecimal. For historical reasons, Python supports programming in octal and hexadecimal. I like to think that the early days of computing were dominated by people with 8 or 16 fingers.

A number with a leading 0 (zero) is octal, base 8, and uses the digits 0 to 7. 0123 is octal and equal to 83 decimal.

A number with a leading 0x or 0X is hexadecimal, base 16, and uses the digits 0 through 9, plus a, A, b, B, c, C, d, D, e, E, f, and F. 0x2BC8 is hexadecimal and equal to 11208.

Hex, octal and long notations can be combined. 0x234C678D098BAL, for example is 620976988526778L.

Function Notation. The absolute value operation is done using a slightly different notation than the conventional mathematical operators like + and - that we saw above. It uses functional notation, sometimes called prefix notation. A mathematician would write | n |. Here's the formal Python definition:

This tells us that abs( x ) has one parameter that must be a numeric value and it returns a numeric value. It won't work with strings or sequences or any of the other Python data types we'll cover in Chapter 11, Sequences: Strings, Tuples and Lists .

Here's an example using the abs( x ) function.

>>> 
print abs(10-28/2)

4

The expression inside the parenthesis is evaluated first (yielding -4). Then the abs( x ) function is applied to -4. This evaluates to 4.

One of the useful data types that Python offers are long integers. Unlike ordinary integers with a limited range, long integers have arbitrary length; they can have as many digits as necessary to represent an exact answer. However, these will operate more slowly than plain integers. Long integers end in L or l. Upper case L is preferred, since the lower-case l looks too much like the digit 1. Python is graceful about converting to long integers when it is necessary.

How many different combinations of 32 bits are there? The answer is there are 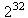different combinations of 32 on-off bits. When we try 2**32 in Python, the answer is too large for ordinary integers, and we get an anwer in long integers.

>>> 
print 2**32

4294967296L

There are about 4 billion ways to arrange 32 bits. How many bits in 1K of memory? 1024×8 bits. How many combinations of bits are possible in 1K of memory?

print 2L**(1024*8)

I won't attempt to reproduce the output from Python. It has 2,467 digits. There are a lot of different combinations of bits in only 1K of memory. The computer I'm using has 256×1024 K of memory; there are a lot of combinations of bits available in that memory.

Python will silently convert between ultra-fast integers and slow-but-large long integers. You can force a conversion using the int or long factory functions.

Python offers floating-point numbers, often implemented as "double-precision" numbers, typically using 64 bits. Floating-point numbers are based on scientific notation, where numbers are written as a mantissa and an exponent. Generally, powers of 10 are used with the exponent, giving us numbers that look like this: .

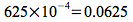When we write a number that includes a decimal point, Python uses floating point representation. We can also use a form of scientific notation with an explicit mantissa and exponent. Here are some examples:

.0625
0.0625
6.25E-2
625E-4

The last example isn't properly normalized, since the mantissa isn't between 0 and 10.

Generally, a number, n , is some mantissa, g , and an exponent of c . For human consumption, we use a base of 10.

Equation 4.1. Scientific Notation

Internally, most computers use a base of 2, not 10. This leads to slight errors in converting certain values, which are exact in base 10, to approximations in base 2.

For example, 1/5th doesn't have a precise representation. This isn't generally a problem because we have string formatting operations which can make this tiny representation error invisible to users.

>>> 
1./5

0.20000000000000001

Besides plain integers, long integers and floating point numbers, Python also provides for imaginary and complex numbers. These use the European convention of ending with J or j. People who don't use complex numbers should skip this section.

3.14J is an imaginary number = .

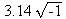A complex number is created by adding a real and an imaginary number: 2 + 14 j . Note that Python always prints these in ()'s; for example (2+14j).

The usual rules of complex math work perfectly with these numbers.

>>> 
print (2+3j)*(4+5j)

(-7+22j)

Python even includes the complex conjugate operation on a complex number. This operation follows the complex number separated by a dot (.). This notation is used because the conjugate is treated like a method function of a complex number object (we'll return to this method and object terminology in Chapter 21, Classes ). For example:

>>> 
print 3+2j.conjugate()

(3-2j)