Section 8.4
Searching and Sorting
TWO ARRAY PROCESSING TECHNIQUES
that are particularly common are
searching and sorting.
Searching here refers to finding an item in the array that
meets some specified criterion. Sorting refers to rearranging all
the items in the array into increasing or decreasing order (where the
meaning of increasing and decreasing can depend on the context).
Sorting and searching are often discussed, in a theoretical sort
of way, using an array of numbers as an example. In practical
situations, though, more interesting types of data are usually
involved. For example, the array might be a mailing list, and
each element of the array might be an object containing a name
and address. Given the name of a person, you might want to
look up that person's address. This is an example of searching,
since you want to find the object in the array that contains the
given name. It would also be useful to be able to sort the
array according to various criteria. One example of sorting
would be ordering the elements of the array so that the names
are in alphabetical order. Another example would be to
order the elements of the array according to zip code before
printing a set of mailing labels. (This kind of sorting can
get you a cheaper postage rate on a large mailing.)
This example can be generalized to a more abstract situation
in which we have an array that contains objects, and we want to search or
sort the array based on the value of one of the instance variables
in that array. We can use some terminology here that originated
in work with "databases," which are just large, organized
collections of data. We refer to each of the objects in the
array as a record. The instance
variables in an object are then called fields
of the record. In the mailing list example, each record would
contain a name and address. The fields of the record might be
the first name, last name, street address, state, city and zip code.
For the purpose of searching or sorting, one of the fields is
designated to be the key field.
Searching then means finding a record in the array that has
a specified value in its key field. Sorting means moving
the records around in the array so that the key fields of the
record are in increasing (or decreasing) order.
In this section, most of my examples follow the tradition of using
arrays of numbers. But I'll also give a few examples using
records and keys, to remind you of the more practical applications.
Searching
There is an obvious algorithm for searching for a particular
item in an array: Look at each item in the array in turn, and
check whether that item is the one you are looking for. If so,
the search is finished. If you look at every item without finding
the one you want, then you can be sure that the item is
not in the array. It's easy to write a subroutine to implement
this algorithm. Let's say the array that you want to search
is an array of ints. Here is a method that will search
the array for a specified integer. If the integer is found,
the method returns the index of the location in the array where
it is found. If the integer is not in the array, the method
returns the value -1 as a signal that the integer could not
be found:
static int find(int[] A, int N) {
// Searches the array A for the integer N.
// Postcondition: If N is not in the array, -1 is
// returned. If N is in the array, then the
// return value, i, is the first integer that
// satisfies A[i] == N.
for (int index = 0; index < A.length; index++) {
if ( A[index] == N )
return index; // N has been found at this index!
}
// If we get this far, then N has not been found
// anywhere in the array. Return a value of -1.
return -1;
}
This method of searching an array by looking at each item
in turn is called linear search.
If nothing is known about the order of the items in the array,
then there is really no better alternative algorithm. But if
the elements in the array are known to be in increasing or decreasing
order, then a much faster search algorithm can be used.
An array in which the elements are in order is said to be
sorted. Of course, it takes some
work to sort an array, but if the array is to be searched many
times, then the work done in sorting it can really pay off.
Binary search is a method for
searching for a given item in a sorted array. Although
the implementation is not trivial, the basic idea is
simple: If you are searching for an item in a sorted list,
then it is possible to eliminate half of the items in the
list by inspecting a single item. For example, suppose that
you are looking for the number 42 in a sorted array of 1000 integers.
Let's assume that the array is sorted into increasing order.
Suppose you check item number 500 in the array, and find that
the item is 93. Since 42 is less than 93, and since the elements in
the array are in increasing order, we can conclude that if 42 occurs in the array
at all, then it must occur somewhere before location 500.
All the locations numbered 500 or above contain values that are greater than
or equal to 93. These locations can be eliminated as possible
locations of the number 42.
The next obvious step is
to check location 250. If the number at that location is, say,
21, then you can eliminate locations before 250 and limit further
search to locations between 251 and 499. The next test will
limit the search to about 125 locations, and the one after that
to about 62. After just 10 steps, there is only one location
left. This is a whole lot better than looking through every
element in the array. If there were a million items, it would still take
only 20 steps for this method to search the array! (Mathematically,
the number of steps is the logarithm, in the base 2, of the number
of items in the array.)
In order to make binary search into a Java subroutine that searches an
array A for an item N, we just have to keep track of the range
of locations that could possibly contain N. At each step,
as we eliminate possibilities, we reduce the size of this range.
The basic operation is to look at the item in the middle of the
range. If this item is greater than N, then the second half of the
range can be eliminated. If it is less than N, then the first half
of the range can be eliminated. If the number in the middle just
happens to be N exactly, then the search is finished. If the size
of the range decreases to zero, then the number N does not occur in the array. Here is
a subroutine that returns the location of N in a sorted array A.
If N cannot be found in the array, then a value of -1
is returned instead:
static int binarySearch(int[] A, int N) {
// Searches the array A for the integer N.
// Precondition: A must be sorted into increasing order.
// Postcondition: If N is in the array, then the return
// value, i, satisfies A[i] == N. If not, then the
// return value is -1.
int lowestPossibleLoc = 0;
int highestPossibleLoc = A.length - 1;
while (highestPossibleLoc >= lowestPossibleLoc) {
int middle = (lowestPossibleLoc + highestPossibleLoc) / 2;
if (A[middle] == N) {
// N has been found at this index!
return middle;
}
else if (A[middle] > N) {
// eliminate locations >= middle
highestPossibleLoc = middle - 1;
}
else {
// eliminate locations <= middle
lowestPossibleLoc = middle + 1;
}
}
// At this point, highestPossibleLoc < LowestPossibleLoc,
// which means that N is known to be not in the array. Return
// a -1 to indicate that N could not be found in the array.
return -1;
}
Association Lists
One particularly common application of searching is with
association lists. The standard example
of an association list is a dictionary. A dictionary
associates definitions with words. Given a word, you can use the
dictionary to look up its definition. We can think of the dictionary
as being a list of pairs of the form
(w,d), where w is a word and d is its definition.
A general association list is a list of pairs (k,v), where
k is some "key" value, and v is a value
associated to that key. In general, we want to assume that no two
pairs in the list have the same key. The basic operation on
association lists is this: Given a key, k, find the value
v associated with k, if any.
Association lists are very widely used in computer science.
For example, a compiler has to keep track of the location in memory
associated with each variable. It can do this with an association list
in which each key is a variable name and the associated value is the
address of that variable in memory. Another example would be a mailing list,
if we think of it as associating an address to each name on the list.
As a related example, consider a phone directory that associates a
phone number to each name. The items in the list could be objects
belonging to the class:
class PhoneEntry {
String name;
String phoneNum;
}
The data for a phone directory consists of an array of type PhoneEntry[]
and an integer variable to keep track of how many entries are actually
stored in the directory. (This is an example of a "partially full array"
as discussed in the previous section. It might
be better to use a dynamic array or an ArrayList to hold the phone
entries.) A phone directory could be an object belonging to the class:
class PhoneDirectory {
PhoneEntry[] info = new PhoneEntry[100]; // Space for 100 entries.
int entries = 0; // Actual number of entries in the array.
void addEntry(String name, String phoneNum) {
// Add a new item at the end of the array.
info[entries] = new PhoneEntry();
info[entries].name = name;
info[entries].phoneNum = phoneNum;
entries++;
}
String getNumber(String name) {
// Return phone number associated with name,
// or return null if the name does not occur
// in the array.
for (int index = 0; index < entries; index++) {
if (name.equals( info[index].name )) // Found it!
return info[index].phoneNum;
}
return null; // Name wasn't found.
}
}
Note that the search method, getNumber, only looks through
the locations in the array that have actually been filled with
PhoneEntries. Also note that unlike the search routines given earlier,
this routine does not return the location of the item in the array.
Instead, it returns the value that it finds associated with the
key, name. This is often done with association lists.
This class could use a lot of improvement. For one thing, it would
be nice to use binary search instead of simple linear search in the
getNumber method. However, we could only do that if the
list of PhoneEntries were sorted into alphabetical order according to
name. In fact, it's really not all that hard to keep the list of
entries in sorted order, as you'll see in just a second.
Insertion Sort
We've seen that there are good reasons for sorting arrays.
There are many algorithms available for doing so. One of the
easiest to understand is the insertion sort
algorithm. This method is also applicable to the problem of keeping
a list in sorted order as you add new items to the list. Let's
consider that case first:
Suppose you have a sorted list and you want to add an item to that
list. If you want to make sure that the modified list is still sorted,
then the item must be inserted into the right location, with all
the smaller items coming before it and all the bigger items after it.
This will mean moving each of the bigger items up one space to make room
for the new item.
static void insert(int[] A, int itemsInArray, int newItem) {
// Precondition: itemsInArray is the number of items that are
// stored in A. These items must be in increasing order
// (A[0] <= A[1] <= ... <= A[itemsInArray-1]).
// The array size is at least one greater than itemsInArray.
// Postcondition: The number of items has increased by one,
// newItem has been added to the array, and all the items
// in the array are still in increasing order.
// Note: To complete the process of inserting an item in the
// array, the variable that counts the number of items
// in the array must be incremented, after calling this
// subroutine.
int loc = itemsInArray - 1; // Start at the end of the array.
/* Move items bigger than newItem up one space;
Stop when a smaller item is encountered or when the
beginning of the array (loc == 0) is reached. */
while (loc >= 0 && A[loc] > newItem) {
A[loc + 1] = A[loc]; // Bump item from A[loc] up to loc+1.
loc = loc - 1; // Go on to next location.
}
A[loc + 1] = newItem; // Put newItem in last vacated space.
}
Conceptually, this could be extended to a sorting method if
we were to take all the items out of an unsorted array, and then
insert them back into the array one-by-one, keeping the list
in sorted order as we do so. Each insertion can be done using the
insert routine given above. In the actual algorithm,
we don't really take all the items from the array; we just remember
what part of the array has been sorted:
static void insertionSort(int[] A) {
// Sort the array A into increasing order.
int itemsSorted; // Number of items that have been sorted so far.
for (itemsSorted = 1; itemsSorted < A.length; itemsSorted++) {
// Assume that items A[0], A[1], ... A[itemsSorted-1]
// have already been sorted. Insert A[itemsSorted]
// into the sorted list.
int temp = A[itemsSorted]; // The item to be inserted.
int loc = itemsSorted - 1; // Start at end of list.
while (loc >= 0 && A[loc] > temp) {
A[loc + 1] = A[loc]; // Bump item from A[loc] up to loc+1.
loc = loc - 1; // Go on to next location.
}
A[loc + 1] = temp; // Put temp in last vacated space.
}
}
The following is an illustration of one stage in insertion sort. It
shows what happens during one execution of the for loop in the
above method, when itemsSorted is 5.
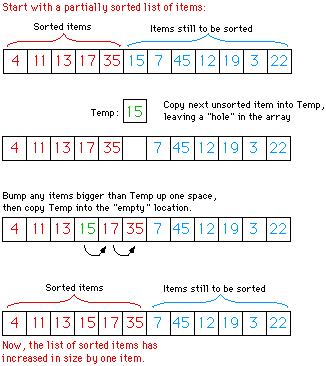
Selection Sort
Another typical sorting method uses the idea of finding the biggest
item in the list and moving it to the end -- which is where it belongs
if the list is to be in increasing order. Once the biggest item is
in its correct location, you can then apply the same idea to the
remaining items. That is, find the next-biggest item, and move it
into the next-to-last space, and so forth. This algorithm is called
selection sort. It's easy to write:
static void selectionSort(int[] A) {
// Sort A into increasing order, using selection sort
for (int lastPlace = A.length-1; lastPlace > 0; lastPlace--) {
// Find the largest item among A[0], A[1], ...,
// A[lastPlace], and move it into position lastPlace
// by swapping it with the number that is currently
// in position lastPlace.
int maxLoc = 0; // Location of largest item seen so far.
for (int j = 1; j <= lastPlace; j++) {
if (A[j] > A[maxLoc]) {
// Since A[j] is bigger than the maximum we've seen
// so far, j is the new location of the maximum value
// we've seen so far.
maxLoc = j;
}
}
int temp = A[maxLoc]; // Swap largest item with A[lastPlace].
A[maxLoc] = A[lastPlace];
A[lastPlace] = temp;
} // end of for loop
}
Insertion sort and selection sort are suitable for sorting
fairly small arrays (up to a few hundred elements, say). There are
more complicated sorting algorithms that are much faster than
insertion sort and selection sort for large arrays. I'll discuss one such
algorithm in Section 11.1.
A variation of selection sort is used in the Hand class
that was introduced in Section 5.3.
(By the way, you are finally in a position to fully understand the source
code for both the Hand class and the Deck class
from that section. See the source files Deck.java
and Hand.java.)
In the Hand class, a hand of playing cards is represented by
a Vector. This is older code, which used Vector instead
of ArrayList, and I have chosen not to modify it so that you would
see at least one example of using Vectors. See the
previous section for a discussion of ArrayLists
and Vectors.
The objects stored in the Vector are of type
Card. A Card object contains instance methods
getSuit() and getValue() that can be used to determine
the suit and value of the card. In my sorting method, I actually create
a new vector and move the cards one-by-one from the old vector to the
new vector. The cards are selected from the old vector in increasing order.
In the end, the new vector becomes the hand and the old vector is discarded.
This is certainly not an efficient procedure! But hands of cards are so
small that the inefficiency is negligible. Here is the code:
public void sortBySuit() {
// Sorts the cards in the hand so that cards of the same
// suit are grouped together, and within a suit the cards
// are sorted by value. Note that aces are considered to have
// the lowest value, 1.
Vector newHand = new Vector();
while (hand.size() > 0) {
int pos = 0; // Position of minimal card.
Card c = (Card)hand.elementAt(0); // Minimal card seen so far.
for (int i = 1; i < hand.size(); i++) {
Card c1 = (Card)hand.elementAt(i);
if ( c1.getSuit() < c.getSuit() ||
(c1.getSuit() == c.getSuit()
&& c1.getValue() < c.getValue()) ) {
pos = i;
c = c1;
}
}
hand.removeElementAt(pos);
newHand.addElement(c);
}
hand = newHand;
}
Unsorting
I can't resist ending this section on sorting with a related
problem that is much less common, but is a bit more fun. That is
the problem of putting the elements of an array into a random
order. The typical case of this problem is shuffling a deck of
cards. A good algorithm for shuffling is similar to selection
sort, except that instead of moving the biggest item to the
end of the list, an item is selected at random and moved to the end
of the list. Here is a subroutine to shuffle an array of ints:
static void shuffle(int[] A) {
// Postcondition: The items in A have been rearranged into
// a random order.
for (int lastPlace = A.length-1; lastPlace > 0; lastPlace--) {
// Choose a random location from among 0,1,...,lastPlace.
int randLoc = (int)(Math.random()*(lastPlace+1));
// Swap items in locations randLoc and lastPlace.
int temp = A[randLoc];
A[randLoc] = A[lastPlace];
A[lastPlace] = temp;
}
}
