Section 11.1
Recursion
AT ONE TIME OR ANOTHER, you've probably been
told that you can't define something in terms of itself. Nevertheless,
if it's done right, defining something at least partially in terms of itself
can be a very powerful technique. A recursive
definition is one that uses the concept or thing that is being defined
as part of the definition. For example: An "ancestor" is either a
parent or an ancestor of a parent. A "sentence" can be, among other
things, two sentences joined by a conjunction such as "and."
A "directory" is a part of a disk drive that can hold files
and directories. In mathematics, a "set" is a collection of
elements, which can be other sets. A "statement" in Java
can be a while statement, which is made up of the
word "while", a boolean-valued condition, and a statement.
Recursive definitions can describe very complex situations
with just a few words. A definition of the term "ancestor" without
using recursion might go something like "a parent, or a grandparent,
or a great-grandparent, or a great-great-grandparent, and so on."
But saying "and so on" is not very rigorous. (I've often thought
that recursion is really just a rigorous way of saying "and so on.")
You run into the same problem if you try to define a "directory"
as "a file that is a list of files, where some of the files can be lists of files,
where some of those files can be lists of files, and so on."
Trying to describe what a Java statement can look like, without using
recursion in the definition, would be difficult and probably pretty
comical.
Recursion can be used as a programming technique.
A recursive subroutine is one
that calls itself, either directly or indirectly. To say
that a subroutine calls itself directly means that its definition
contains a subroutine call statement that calls the subroutine that
is being defined. To say that a subroutine calls itself indirectly
means that it calls a second subroutine which in turn calls the
first subroutine (either directly or indirectly).
A recursive subroutine can define a complex task in just
a few lines of code. In the rest of this section, we'll look
at a variety of examples, and we'll see other examples in
the remaining sections of this chapter.
Let's start with an example that you've seen before:
the binary search algorithm from Section 8.4.
Binary search is used to find a specified value in a sorted list of items
(or, if it does not occur in the list, to determine that fact).
The idea is to test the element in the middle of the list. If that element
is equal to the specified value, you are done. If the specified value
is less than the middle element of the list, then you should search
for the value in the first half of the list. Otherwise, you
should search for the value in the second half of the list.
The method used to search for the value in the first or second
half of the list is binary search. That is, you look at the middle
element in the half of the list that is still under consideration, and either
you've found the value you are looking for, or you have to apply binary
search to one half of the remaining elements. And so on!
This is a recursive description, and we can write a recursive
subroutine to implement it.
Before we can do that, though, there are two considerations that we need
to take into account. Each of these illustrates an important general
fact about recursive subroutines. First of all, the binary search
algorithm begins by looking at the "middle element of the list."
But what if the list is empty? If there are no elements in the
list, then it is impossible to look at the middle element. In the
terminology of Section 9.2, having a
non-empty list is a "precondition" for looking at the middle element,
and this is a clue that we have to modify the algorithm to take
this precondition into account. What should we do if we find ourselves
searching for a specified value in an empty list? The answer is easy:
We can say immediately that the value does not occur in the list.
An empty list is a base case for the
binary search algorithm. A base case for a recursive algorithm is
a case that is handled directly, rather than by applying the algorithm
recursively. The binary search algorithm actually has another
type of base case: If we find the element we are looking for in
the middle of the list, we are done. There is no need for further
recursion.
The second consideration has to do with the parameters to the
subroutine. The problem is phrased in terms of searching for a value in
a list. In the original, non-recursive binary search subroutine,
the list was given as an array. However, in the recursive
approach, we have to able to apply the subroutine recursively to
just a part of the original list. Where the original subroutine
was designed to search an entire array, the recursive subroutine
must be able to search part of an array. The parameters to the
subroutine must tell it what part of the array to search. This illustrates
a general fact that in order to solve a problem recursively, it is
often necessary to generalize the problem slightly.
Here is a recursive binary search algorithm that searches for
a given value in part of an array of integers:
static int binarySearch(int[] A, int loIndex, int hiIndex, int value) {
// Search in the array A in positions from loIndex to hiIndex,
// inclusive, for the specified value. It is assumed that the
// array is sorted into increasing order. If the value is
// found, return the index in the array where it occurs.
// If the value is not found, return -1.
if (loIndex > hiIndex) {
// The starting position comes after the final index,
// so there are actually no elements in the specified
// range. The value does not occur in this empty list!
return -1;
}
else {
// Look at the middle position in the list. If the
// value occurs at that position, return that position.
// Otherwise, search recursively in either the first
// half or the second half of the list.
int middle = (loIndex + hiIndex) / 2;
if (value == A[middle])
return middle;
else if (value < A[middle])
return binarySearch(A, loIndex, middle - 1, value);
else // value must be > A[middle]
return binarySearch(A, middle + 1, hiIndex, value);
}
} // end binarySearch()
In this routine, the parameters loIndex and hiIndex
specify the part of the array that is to be searched. To search an
entire array, it is only necessary to call
binarySearch(A, 0, A.length - 1, value).
In the two base cases -- where there are no elements in the specified
range of indices and when the value is found in the middle of the range --
the subroutine can return an answer immediately, without using recursion.
In the other cases, it uses a recursive call to compute the answer and
returns that answer.
Most people find it difficult at first to convince themselves that
recursion actually works. The key is to note two things that
must be true for recursion to work properly: There must be one
or more base cases, which can be handled without using recursion.
And when recursion is applied during the solution of a problem,
it must be applied to a problem that is in some sense smaller -- that
is, closer to the base cases -- than the original problem. The idea is
that if you can solve small problems and if you can reduce big problems
to smaller problems, then you can solve problems of any size.
Ultimately, of course, the big problems have to be reduced, possibly
in many, many steps, to the very smallest problems (the base cases).
Doing so might involve an immense amount of detailed bookkeeping.
But the computer does that bookkeeping, not you! As a programmer,
you lay out the big picture: the base cases and the reduction of
big problems to smaller problems. The computer takes care of the
details involved in reducing a big problem, in many steps, all the
way down to base cases. Trying to think through this reduction in
detail is likely to drive you crazy, and will probably make you think
that recursion is hard. Whereas in fact, recursion is an elegant and
powerful method that is often the simplest approach to solving a
complex problem.
A common error in writing recursive subroutines is to violate
one of the two rules: There must be one or more base cases,
and when the subroutine is applied recursively, it must be applied
to a problem that is smaller than the original problem. If these
rules are violated, the result can be an infinite
recursion, where the subroutine keeps calling itself over and
over, without ever reaching a base case. Infinite recursion is
similar to an infinite loop. However, since each recursive call to
the subroutine uses up some of the computer's memory, a program that
is stuck in an infinite recursion will run out of memory and crash
before long. (In Java, the program will crash with an exception of
type StackOverflowError.)
Binary search can be implemented with a while loop,
instead of with recursion, as was done in Section 8.4.
Next, we turn to a problem that is easy to solve with recursion but
difficult to solve without it. This is a standard example known
as "The Towers of Hanoi". The problem involves a stack of various-sized
disks, piled up on a base in order of decreasing size. The object is to
move the stack from one base to another, subject to two rules:
Only one disk can be moved at a time, and no disk can ever be placed
on top of a smaller disk. There is a third base that can
be used as a "spare". The situation for a stack of ten disks is
shown in the top half of the following picture. The situation after
a number of moves have been made is shown in the bottom half of the
picture. These pictures are from the applet at the end of
Section 10.5, which displays
an animation of the step-by-step solution of the problem.
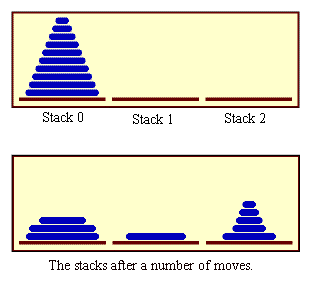
The problem is to move ten disks from Stack 0 to Stack 1, subject
to certain rules. Stack 2 can be used a spare location. Can we reduce
this to smaller problems of the same type, possibly generalizing the
problem a bit to make this possible? It seems natural to consider
the size of the problem to be the number of disks to be moved. If there
are N disks in Stack 0, we know that we will eventually have
to move the bottom disk from Stack 0 to Stack 1. But before we can
do that, according to the rules, the first N-1 disks must be
on Stack 2. Once we've moved the N-th disk to Stack 1,
we must move the other N-1 disks from Stack 2 to Stack 1
to complete the solution. But moving N-1 disks is the same
type of problem as moving N disks, except that it's a smaller
version of the problem. This is exactly what we need to do recursion!
The problem has to be generalized a bit, because the smaller problems
involve moving disks from Stack 0 to Stack 2 or from Stack 2 to Stack 1,
instead of from Stack 0 to Stack 1. In the recursive subroutine
that solves the problem, the stacks that serve as the source and
destination of the disks have to be specified. It's also convenient
to specify the stack that is to be used as a spare, even though we
could figure that out from the other two parameters. The
base case is when there is only one disk to be moved. The solution in
this case is trivial: Just move the disk in one step. Here is a
version of the subroutine that will print out step-by-step instructions
for solving the problem:
void TowersOfHanoi(int disks, int from, int to, int spare) {
// Solve the problem of moving the number of disks specified
// by the first parameter from the stack specified by the
// second parameter to the stack specified by the third
// parameter. The stack specified by the fourth parameter
// is available for use as a spare.
if (disks == 1) {
// There is only one disk to be moved. Just move it.
System.out.println("Move a disk from stack number "
+ from + " to stack number " + to);
}
else {
// Move all but one disk to the spare stack, then
// move the bottom disk, then put all the other
// disks on top of it.
TowersOfHanoi(disks-1, from, spare, to);
System.out.println("Move a disk from stack number "
+ from + " to stack number " + to);
TowersOfHanoi(disks-1, spare, to, from);
}
}
This subroutine just expresses the natural recursive solution.
The recursion works because each recursive call involves a smaller
number of disks, and the problem is trivial to solve in the base
case, when there is only one disk. To solve the "top level"
problem of moving N disks from Stack 0 to Stack 1,
it should be called with the command TowersOfHanoi(N,0,1,2).
Here is an applet that uses this subroutine. You can specify the
number of disks. Be careful. The number of steps increases rapidly
with the number of disks.
What this applet shows you is a mass of detail that you don't
really want to think about! The difficulty of following the details
contrasts sharply with the simplicity and elegance of the recursive solution.
Of course, you really want to leave the details to the computer.
It's much more interesting to watch the applet from Section 10.5,
which shows the solution graphically.
That applet uses the same recursive subroutine, except
that the System.out.println
statements are replaced by commands that show the image of the disk
being moved from one stack to another. You can find the complete
source code in the file TowersOfHanoi.java.
There is, by the way, a story that explains the name of this problem.
According to this story, on the first day of creation, a group of monks
in an isolated tower near Hanoi were given a stack of 64 disks and were
assigned the task of moving one disk every day, according to the rules
of the Towers of Hanoi problem. On the day that they complete their
task of moving all the disks from one stack to another, the universe will
come to an end. But don't worry. The number of steps required to solve
the problem for N disks is 2N - 1, and
264 - 1 days is over 50,000,000,000,000 years.
We have a long way to go.
Turning next to an application that is perhaps more practical,
we'll look at a recursive algorithm for sorting an array. The
selection sort and insertion sort algorithm algorithms, which were
covered in Section 8.4, are fairly simple,
but they are rather slow when applied to large arrays. Faster
sorting algorithms are available. One of these is Quicksort, a
recursive algorithm which turns out to be the fastest sorting algorithm
in most situations.
The Quicksort algorithm is based on a simple but clever idea:
Given a list of items, select any item from the list. This
item is called the pivot. (In practice,
I'll just use the first item in the list.) Move all the
items that are smaller than the pivot to the beginning
of the list, and move all the items that are larger than the
pivot to the end of the list. Now, put the pivot
between the two groups of items. This puts the pivot in the
position that it will occupy in the final, completely sorted array.
It will not have to be moved again. We'll refer to this procedure
as QuicksortStep.

QuicksortStep is not recursive. It is used as a subroutine by
Quicksort. The speed of Quicksort depends on having a fast implementation
of QuicksortStep. Since it's not the main point of this discussion,
I present one without much comment.
static int quicksortStep(int[] A, int lo, int hi) {
// Apply QuicksortStep to the list of items in
// locations lo through hi in the array A. The value
// returned by this routine is the final position
// of the pivot item in the array.
int pivot = A[lo]; // Get the pivot value.
// The numbers hi and lo mark the endpoints of a range
// of numbers that have not yet been tested. Decrease hi
// and increase lo until they become equal, moving numbers
// bigger than pivot so that they lie above hi and moving
// numbers less than the pivot so that they lie below lo.
// When we begin, A[lo] is an available space, since it used
// to hold the pivot.
while (hi > lo) {
while (hi > lo && A[hi] > pivot) {
// Move hi down past numbers greater than pivot.
// These numbers do not have to be moved.
hi--;
}
if (hi == lo)
break;
// The number A[hi] is less than pivot. Move it into
// the available space at A[lo], leaving an available
// space at A[hi].
A[lo] = A[hi];
lo++;
while (hi > lo && A[lo] < pivot) {
// Move lo up past numbers less than pivot.
// These numbers do not have to be moved.
lo++;
}
if (hi == lo)
break;
// The number A[lo] is greater than pivot. Move it into
// the available space at A[hi], leaving an available
// space at A[lo].
A[hi] = A[lo];
hi--;
} // end while
// At this point, lo has become equal to hi, and there is
// an available space at that position. This position lies
// between numbers less than pivot and numbers greater than
// pivot. Put pivot in this space and return its location.
A[lo] = pivot;
return lo;
} // end QuicksortStep
With this subroutine in hand, Quicksort is easy. The Quicksort algorithm
for sorting a list consists of applying QuicksortStep to the list,
then applying Quicksort recursively to the items that lie to the left
of the pivot and to the items that lie to the right of the pivot.
Of course, we need base cases. If the list has only one item, or no items,
then the list is already as sorted as it can ever be, so Quicksort
doesn't have to do anything in these cases.
static void quicksort(int[] A, int lo, int hi) {
// Apply quicksort to put the array elements between
// position lo and position hi into increasing order.
if (hi <= lo) {
// The list has length one or zero. Nothing needs
// to be done, so just return from the subroutine.
return;
}
else {
// Apply quicksortStep and get the pivot position.
// Then apply quicksort to sort the items that
// precede the pivot and the items that follow it.
int pivotPosition = quicksortStep(A, lo, hi);
quicksort(A, lo, pivotPosition - 1);
quicksort(A, pivotPosition + 1, hi);
}
}
As usual, we had to generalize the problem. The original problem was
to sort an array, but the recursive algorithm is set up to sort a
specified part of an array. To sort an entire array, A,
using the quickSort() subroutine, you would call
quicksort(A, 0, A.length - 1).
Here's an applet that shows a grid of little squares. The
gray squares are "filled" and the white squares are "empty."
For the purposes of this applet, we define a "blob" to consist
of a filled square and all the filled squares that can be reached
from it by moving up, down, left, and right through other filled
squares. If you click on any filled square in the applet,
the computer will count the squares in the blob that contains
it, and it will change the color of those squares
to red. Click on the "New Blobs" button to create a new random
pattern in the grid. The pop-up menu gives the approximate
percentage of squares that will be filled in the new pattern.
The more filled squares, the larger the blobs. The button labeled
"Count the Blobs" will tell you how many different blobs there are
in the pattern.
Recursion is used in this applet to count the number of squares in
a blob. Without recursion, this would be a very difficult
thing to program. Recursion makes it relatively easy, but
it still requires a new technique, which is also useful in a number
of other applications.
The data for the grid of squares is stored in a two dimensional
array of boolean values,
boolean[][] filled;
The value of filled[r][c] is true if the
square in row r and in column c of the grid
is filled. The number of rows in the grid is stored in an
instance variable named rows, and the number of
columns is stored in columns. The applet uses
a recursive instance method named getBlobSize()
to count the number of squares in the blob that contains the
square in a given row r and column c.
If there is no filled square at position (r,c),
then the answer is zero. Otherwise,
getBlobSize() has to count all the filled squares
that can be reached from the square at position (r,c).
The idea is to use getBlobSize() recursively to
get the number of filled squares that can be reached from
each of the neighboring positions, (r+1,c),
(r-1,c), (r,c+1), and (r,c-1).
Add up these numbers, and add one to count the square
at (r,c) itself, and you get the total number of
filled squares that can be reached from (r,c).
Here is an implementation of this algorithm, as stated.
Unfortunately, it has a serious flaw: It leads to an
infinite recursion!
int getBlobSize(int r, int c) { // BUGGY, INCORRECT VERSION!!
// This INCORRECT method tries to count all the filled
// squares that can be reached from position (r,c) in the grid.
if (r < 0 || r >= rows || c < 0 || c >= columns) {
// This position is not in the grid, so there is
// no blob at this position. Return a blob size of zero.
return 0;
}
if (filled[r][c] == false) {
// This square is not part of a blob, so return zero.
return 0;
}
int size = 1; // Count the square at this position, then count the
// the blobs that are connected to this square
// horizontally or vertically.
size += getBlobSize(r-1,c);
size += getBlobSize(r+1,c);
size += getBlobSize(r,c-1);
size += getBlobSize(r,c+1);
return size;
} // end INCORRECT getBlobSize()
Unfortunately, this routine will count the same square more than once. In fact,
it will try to count each square infinitely often! Think of yourself
standing at position (r,c) and trying to follow these instructions.
The first instruction tells you to move up one row. You do that,
and then you apply the same procedure.
As one of the steps in that procedure, you have to move
down one row and apply the same procedure yet again. But that puts you
back at position (r,c)! From there, you move up one row,
and from there you move down one row.... Back and forth forever!
We have to make sure that a square is only counted and processed
once, so we don't end up going around in circles. The solution is
to leave a trail of breadcrumbs -- or on the computer a trail of
boolean variables -- to mark the squares that you've already visited.
Once a square is marked as visited, it won't be processed again.
The remaining, unvisited squares are reduced in number, so definite
progress has been made in reducing the size of the problem. Infinite
recursion is avoided!
Another boolean array, visited[r][c], is used to keep track
of which squares have already been visited and processed. It is assumed
that all the values in this array are set to false before getBlobSize()
is called. As getBlobSize() encounters unvisited squares,
it marks them as visited by setting the corresponding entry in the
visited array to true. When getBlobSize()
encounters a square that is already visited, it doesn't count it or
process it further. The technique of "marking" items as they are
encountered is one that used over and over in the programming of
recursive algorithms. Here is the corrected version of getBlobSize(),
with changes shown in red:
int getBlobSize(int r, int c) {
// Counts the squares in the blob at position (r,c) in the
// grid. Squares are only counted if they are filled and
// unvisited. If this routine is called for a position that
// has been visited, the return value will be zero.
if (r < 0 || r >= rows || c < 0 || c >= columns) {
// This position is not in the grid, so there is
// no blob at this position. Return a blob size of zero.
return 0;
}
if (filled[r][c] == false || visited[r][c] == true) {
// This square is not part of a blob, or else it has
// already been counted, so return zero.
return 0;
}
visited[r][c] = true; // Mark the square as visited so that
// we won't count it again during the
// following recursive calls.
int size = 1; // Count the square at this position, then count the
// the blobs that are connected to this square
// horizontally or vertically.
size += getBlobSize(r-1,c);
size += getBlobSize(r+1,c);
size += getBlobSize(r,c-1);
size += getBlobSize(r,c+1);
return size;
} // end getBlobSize()
In the applet, this method is used to determine the size of a blob
when the user clicks on a square. After getBlobSize() has
performed its task, all the squares in the blob are still marked
as visited. The paintComponent() method draws visited squares
in red, which makes the blob visible. The getBlobSize()
method is also used for counting blobs. This is done by the following
method, which includes comments to explain how it works:
void countBlobs() {
// When the user clicks the "Count the Blobs" button, find the
// number of blobs in the grid and report the number in the
// message Label.
int count = 0; // Number of blobs.
/* First clear out the visited array. The getBlobSize() method
will mark every filled square that it finds by setting the
corresponding element of the array to true. Once a square
has been marked as visited, it will stay marked until all the
blobs have been counted. This will prevent the same blob from
being counted more than once. */
for (int r = 0; r < rows; r++)
for (int c = 0; c < columns; c++)
visited[r][c] = false;
/* For each position in the grid, call getBlobSize() to get the
size of the blob at that position. If the size is not zero,
count a blob. Note that if we come to a position that was part
of a previously counted blob, getBlobSize() will return 0 and
the blob will not be counted again. */
for (int r = 0; r < rows; r++)
for (int c = 0; c < columns; c++) {
if (getBlobSize(r,c) > 0)
count++;
}
repaint(); // Note that all the filled squares will be red,
// since they have all now been visited.
message.setText("The number of blobs is " + count);
} // end countBlobs()
You can find the complete source code for the applet in the
file Blobs.java.
Among the decorative end-of-chapter applets in this text,
there are two others that use recursion: The maze-solving
applet from the end of Section 8.5
and the pentominos applet from the end of Section 5
in this chapter.
The Maze applet first builds a random maze. It then tries to solve
the maze by finding a path through the maze from the upper left corner
to the lower right corner. This problem is actually very similar to
the blob-counting problem. The recursive maze-solving routine starts from
a given square, and it visits each neighboring square and calls itself
recursively from there. The recursion ends if the routine finds itself
at the lower right corner of the maze.
The Pentominos applet is an implementation of a classic puzzle.
A pentomino is a connected figure made up of five equal-sized squares.
There are exactly twelve figures that can be made in this way, not
counting all the possible rotations and reflections of the basic
figures. The problem is to place the twelve pentominos on an
8-by-8 board in which four of the squares have already been marked
as filled. The recursive solution looks at a board that has already
been partially filled with pentominos. The subroutine looks at
each remaining piece in turn. It tries to place that piece in the
next available place on the board. If the piece fits, it calls itself
recursively to try to fill in the rest of the solution. If that fails,
then the subroutine goes on to the next piece. (By the way, if you
click on the Pentominos applet, it will start over with a new,
randomly chosen problem.)
The Maze applet and the Pentominos applet are fun to watch, and
they give nice visual representations of recursion.
We'll encounter other examples of recursion later in this chapter.
