5.6.5 The Hue, Saturation, Value, and Color Blending Modes
The Hue, Saturation, Value, and Color blending modes all work similarly. For each mode, one
HSV component is taken from the foreground pixel and the other two
components from the background pixel. For example, if the Hue
blending mode is chosen, the result is the hue of the foreground
pixels combined with the saturation and value of the background
pixels. The same process is used for the Saturation and Value blending modes. The Color blending mode, however, is
slightly different. For this mode, the hue and saturation of the
foreground pixels are used in conjunction with the
lightness of the background pixels. Lightness,
defined in Section
5.3, is less bright than
value, and is simultaneously more true to the human perception of
brightness.
Thus, the action of the Hue blending mode can be expressed as
R=[h(F),s(B),v(B)]
where
h(
F) means the hue of the foreground,
s(
B) represents the
saturation of the background, and
v(
B) is the value of the
background. An example of applying the
Hue blending mode is
illustrated in Figure
5.20.
Figure 5.20:
An Example of Hue Mode
 |
The flower image from Figure
5.15(a) is shown
in Figure
5.20(a). This image is the
foreground to the
Hue mode, and the background is the blue layer
shown in Figure
5.20(b). This blue layer
varies horizontally in value and vertically in saturation. The result
of applying the
Hue mode is shown in
Figure
5.20(c). Here, it can be clearly seen
that the saturation and value variations of the blue layer are
combining with the hue of the flower layer.
Similar to Hue, the Saturation blending mode produces
resultant pixels that are a combination of the saturation of the
foreground and the hue and value of the background. The expression
for this is
R=[h(B),s(F),v(B)]
where
s(
F) is the saturation of the foreground,
h(
B) is the hue of
the background, and
v(
B) represents the value of the background. An
example of applying the
Saturation blending mode is illustrated
in Figure
5.21.
Figure 5.21:
An Example of Saturation Mode
 |
We see again our flower image in
Figure
5.21(a) playing the role of the
foreground layer. However, now the background layer, shown in
Figure
5.21(b), has been constructed to
vary only in hue and value. In this layer, the hue changes along the
horizontal direction and the value along the vertical. The result of
applying the
Saturation mode is shown in
Figure
5.21(c).
The Value blending mode produces resultant pixels that are a
combination of the value of the foreground and the hue and saturation
of the background. The expression for this is
R=[h(B),s(B),v(F)]
Here,
v(
F) represents the foreground value,
h(
B) the background hue,
and
s(
B) the background saturation. An example of this blending
mode is shown in Figure
5.22.
Figure 5.22:
An Example of Value Mode
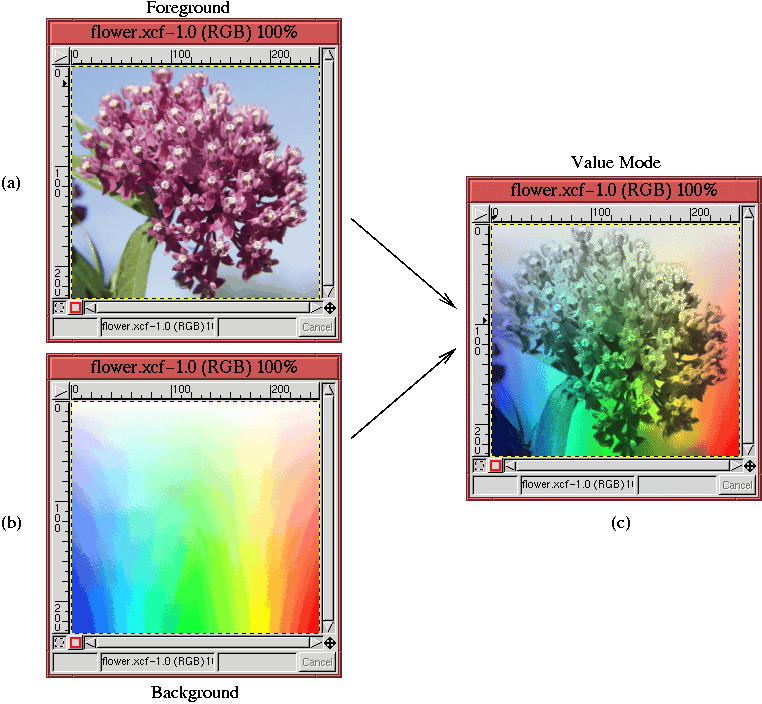 |
The background layer, shown in
Figure
5.22(b), varies in hue in the
horizontal direction and saturation in the vertical direction. The
result of this mode is shown in
Figure
5.22(c).
The final example in this section illustrates the Color blending
mode. This mode combines the foreground hue and saturation with the
background lightness. Lightness was defined earlier in
Section
5.3; lightness is always a bit less
bright than value. The expression for this blending mode is
R=[h(F),s(F),l(B)]
where
h(
F) and
s(
F) are the hue and saturation of the foreground,
and
l(
B) is the lightness of the background. An example of this
blending mode is shown in Figure
5.23.
Figure 5.23:
An Example of Color Mode
 |
Here, the background, shown in
Figure
5.23(b), varies only in value. The
result is shown in Figure
5.23(c).
©2000 Gimp-Savvy.com
