5.6.2 The Addition, Subtract, and Difference Blending Modes
Addition, Subtract, and Difference are blending
modes that add and subtract foreground and background pixel values in
RGB colorspace. Figure
5.14
Figure 5.14:
Addition and Subtraction in the RGB Cube
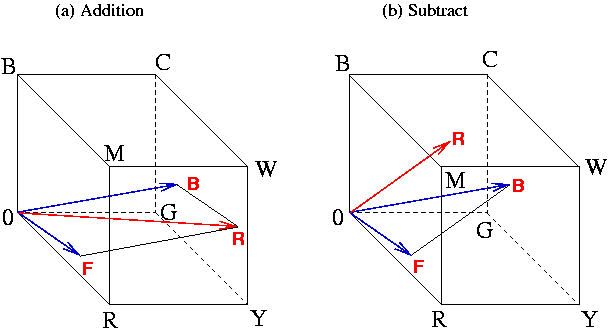 |
illustrates the effect of addition and subtraction for two pixels in the
RGB cube.
The Addition blending mode works as follows. Given a foreground
and background pixel, represented by the RGB vectors
F=[r1,g1,b1]and
B=[r2,g2,b2], the pixel obtained from the Addition
blending mode is
R=F+B=[r1+r2,g1+g2,b1+b2]. Thus, in
Figure
5.14(a), the two blue arrows
represent a foreground and background pixel, and the red arrow is the
vector sum of the two. Addition always produces a resultant color
that is as light or lighter than either the foreground or background
colors. This is because the vector sum must have a projection onto
the neutral axis that is closer to white than the projection for
either the background or foreground colors.
In the event that the vector sum produces a result outside of the
color cube (that is, by producing any RGB component greater than 255),
its value is clipped to the surface of the cube. The equation
describing the Addition blending mode is
where
W is the vector
[255,255,255] and the
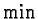
function
performs component-wise minimization of the two vectors.
Cyan, magenta, and yellow are the sums of green and blue, red and
blue, and red and green, respectively. Thus, cyan, magenta, and
yellow appear lighter than red, green, or blue because they project
higher up onto the neutral axis. Furthermore, any of these secondary
colors (cyan, magenta, yellow) summed with the complementary primary
color (red, green, blue) produces white, the lightest color of all.
Figure
5.15
Figure 5.15:
Using the Addition Blending Mode
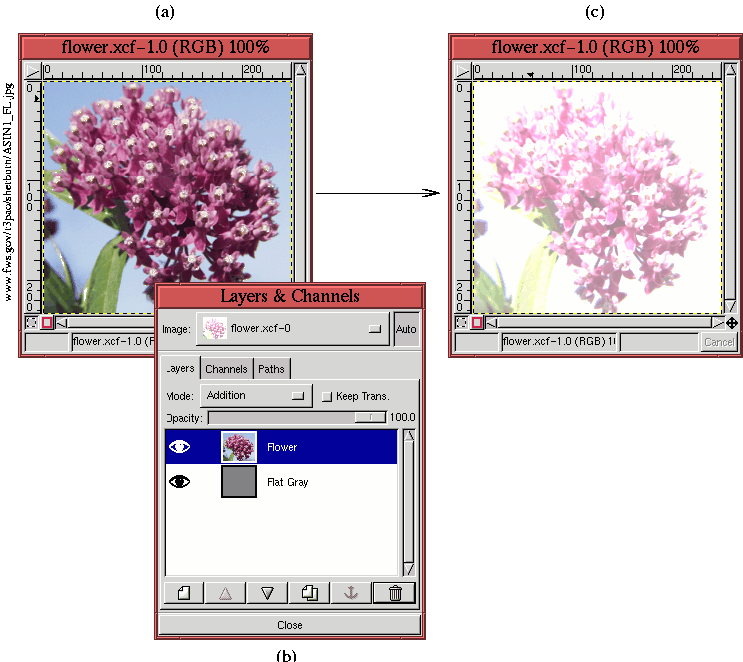 |
illustrates an application of the
Addition blending mode.
Figure
5.15(a) displays the image of a flower,
and Figure
5.15(b), showing the associated
Layers dialog, indicates that this image consists of two-layers. The
upper layer is the flower image, and the lower layer is filled with a
medium gray whose pixel values are uniformly
127
R 127
G 127
B.
Figure
5.15(a) shows the flower image for the
Normal blending mode. Figure
5.15(c)
shows the same image when the blending mode of the upper layer is
changed to Addition. This has the effect of adding
127R 127G
127B to every pixel in the flower layer, which lightens the entire
image considerably. In fact, some parts of the image are completely
blown out to white.
The effect of the Subtract blending mode is illustrated in
Figure
5.14(b). This blending mode works
as follows. Given a foreground and background pixel, we'll again
represent each as an RGB vector
F=[r1,g1,b1] and
B=[r2,g2,b2]. The pixel obtained from the Subtract
blending mode is
R=B-F=[r2-r1,g2-g1,b2-b1]. Thus, for the two
blue arrows labeled F and B in
Figure
5.14(b), the result of subtracting
the foreground from the background is given by the red arrow labeled
R.
Unlike the Addition blending mode, Subtract is not
symmetrical (that is, subtracting F from B is not the same as
subtracting B from F). The result of subtracting the foreground
from the background can produce negative values. If a component of
the resulting RGB vector is less than zero, it is clipped to the
surface of the cube. Thus, the equation representing the Subtract blending mode is
where 0 represents the color
0
R 0
G 0
B and
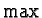
is the
function that performs component-wise maximization of the two vectors.
Because the foreground color is always a positive number, the result
is always darker than the background (unless either the foreground or
background are black, and then there is no change).
The Difference blending mode is like Subtract, but the
result is symmetrical between the foreground and the background. Difference is symmetrical because it applies an absolute value to the
difference of the foreground and background values. Thus, if one of
the RGB components is negative after subtraction, its sign is reversed
to make it positive. The resulting mathematical expression for the
Difference blending mode is
R=|F-B|
where the vertical bars in the equation represent the absolute value
function.
Figure
5.16
Figure 5.16:
Using the Subtract and Difference Blending Modes
 |
illustrates the application of the
Subtract and
Difference
blending modes. The modes are applied to the image from
Figure
5.15(a), which consists of the flower
in the upper layer and a medium gray in the lower layer. You can see
that the result of using
Subtract, shown in
Figure
5.16(a), has regions that
are totally black. This is where the difference between the
foreground and background creates negative values that are clipped to
zero.
Difference, shown in
Figure
5.16(b), however, has no
clipped values because it employs the absolute value of the
difference. Note that for both the
Subtract and
Difference modes, the results are darker than the original flower
image.
