Grokking The Gimp
Previous Page	Home	Next Page

         
5.6.3 The Multiply (Burn), Divide (Dodge), Screen, and Overlay Blending Modes

Multiply, Divide, Screen, and Overlay are all multiplicative blending modes. The resulting pixel values are the product or a function of the product of the foreground and background pixels.

The actions of the Multiply and Screen modes on pixels represented in the RGB cube are illustrated in Figure  5.17.

For a foreground pixel whose position in the RGB cube is [r₁,g₁,b₁] and a background pixel whose position is [r₂,g₂,b₂], the resultant pixel for Multiply mode is the component-by-component product of the two, or [r₁r₂/255,g₁g₂/255,b₁b₂/255], where the division by 255 is necessary to normalize the result back into the RGB cube. This can be succinctly expressed by the equation

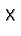
where the symbol means component-wise multiplication.

Due to the scale factor of 255, the component values of one RGB vector are normalized to the range [0,1]. Thus, R is component-wise smaller than either F or B. From previous discussions, you know that smaller means darker because the projection onto the neutral axis is closer to the origin. This is illustrated in Figure  5.17(a) which shows two blue arrows representing the foreground and background pixel positions and a red arrow representing the component-wise product.

Figure  5.18(a)

illustrates an example of applying Multiply mode to the flower image from Figure  5.15(a). As before, the lower layer of this image is a uniform gray equal to 127^R 127^G 127^B. The result, shown in Figure  5.18(a), is the image has been made uniformly darker. In fact, because the lower layer is a medium gray, the pixels values in the flower layer have been scaled by everywhere.

For a foreground pixel whose position in the RGB cube is [r₁,g₁,b₁] and a background pixel whose position is [r₂,g₂,b₂], you might imagine that the resultant pixel for the Divide blending mode would be analogous to that for the Multiply mode. This would suggest something like [255r₂/r₁,255g₂/g₁,255b₂/b₁]. However, this expression presents two problems. The first problem is that when the foreground pixel has a zero component, the result is not defined; the second problem is that when the foreground pixel value is small, the result can be so large that it is no longer inside the RGB cube. The first problem is solved by adding one to each component of the foreground pixel. This prevents a division by zero. The second problem is solved by clipping values that are too large to the surface of the cube.

A succinct expression for the Divide mode is

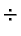
where W is 255^R 255^G 255^B, represents component-wise division of two vectors, and represents component-wise minimization. Figure  5.18(b) illustrates the application of Divide to the flower image from Figure  5.15(a). Here, you can see that some parts of the resulting image are blown out to white. This occurs in regions where the original flower image has small (that is dark) pixel values. Note that Divide always lightens an image because, it divides each pixel component by a number less than 1.

The Screen blending mode has a lightening effect that is exactly analogous to the darkening effect created by Multiply. This concept is illustrated in Figure  5.17(b). As shown in the figure Screen mode redefines the origin to be 255^R 255^G 255^B, the white point in the cube. Thus, the vectors to the foreground and background pixels are as shown by the two blue arrows in Figure  5.17(b). Screen then multiplies the two vectors, producing a resultant shown as a red arrow in Figure  5.17(b). As with the Multiply mode, the resulting vector of the Screen mode is shorter than either the foreground or background vectors--but with respect to the white point in the cube. Thus, the resulting vector is closer to the white point, and, consequently, lighter than either the foreground or background colors. The mathematical expression for Screen mode is

Again, the factor of 255 is introduced to keep the resultant pixel values inside the RGB cube.

Figure  5.18(c) illustrates an example of applying the Screen mode to the flower image from Figure  5.15(a). As predicted, the result is everywhere brighter than in the original image of the flower. Also notice that unlike Divide, Screen mode does not blow out to white. Thus, although both Divide and Screen have similar lightening characteristics, they have very different personalities.

Finally, the Overlay mode is a combination of both Multiply and Screen. The equation for overlay mode is

where R_s represents the resultant pixel value for Screen mode and R_m represents that for Multiply. This equation says that the resultant pixel value for Overlay mode is a combination of the Screen and Multiply modes. The mix of the two modes is proportional to the background pixel value.

Thus, if the background is dark (that is, has an RGB value close to zero in all three components), the result of Multiply mode will dominate and the result of Screen mode will be suppressed. The opposite is true if the background pixel is light (that is, has an RGB value close to white in all three components). Overall, Overlay mode tends to make an image darker where it is already dark and lighter where it is already light. Figure  5.18(d) illustrates an example of applying Overlay mode to the flower image from Figure  5.15(a).

Grokking The Gimp
Previous Page	Home	Next Page