For those programmers new to statistics, this section provides background on the Sigma operator, Σ.

Equation 13.3. Basic Summation

The Σ operator has three parts to it. Below it is a bound variable, i and the starting value for the range, written as i =0. Above it is the ending value for the range, usually something like n . To the right is some function to execute for each value of the bound variable. In this case, a generic function, f ( i ). This is read as “sum f ( i ) for i in the range 0 to n ”.

One common definition of Σ uses a closed range, including the end values of 0 and n . However, since this is not a helpful definition for software, we will define Σ to use a half-open interval. It has exactly n elements, including 0 and n -1; mathematically, .

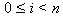Consequently, we prefer the following notation, but it is not often used. Most statistical and mathematical texts seem to use 1-based indexing, consequently some care is required when translating formulae to programming languages that use 0-based indexing.

Equation 13.4. Summation with Half-Open Interval

Our two statistical algorithms have a form more like the following. In this we are applying some function, f (), to each value, x_i of an array. When computing the mean, there is no function. When computing standard deviation, the function involves subtracting and multiplying.

Equation 13.5. Summing Elements of an Array, x

We can transform this definition directly into a for loop that sets the bound variable to all of the values in the range, and does some processing on each value of the list of integers. This is the Python implemention of Sigma. This computes two values, the sum, sum, and the number of elements, n.

Example 13.2. Python Sigma Iteration

sum= 0
for i in range(len(theList)): 


    xi= theList[i] 


    
# fxi = processing of xi
  


    sum += fxi
n= len(theList)

	Get the length of theList. Execute the body of the loop for all values of i in the range 0 to the number of elements-1.
	Fetch item i from theList and assign it to xi.
	For simple mean calculation, this statement does nothing. For standard deviation, however, this statement computes the measure of deviation from the average.

More advanced Python programmers may be aware that there are several ways to shorten this loop down to a single expression using the reduce function as well as list comprehensions.

An Optimization. In the usual mathematical notation, an integer index, i is used. In Python it isn't necessary to use the formal integer index. Instead, an iterator can be used to visit each element of the list, without actually using an explicit numeric counter. The processing simplifies to the following.

Example 13.3. Python Sample Values by Iterator

for xi in theList: 


    
# fxi = processing of xi
 


    sum += fxi
n= len(theList)

	Execute the loop assigning each item of of theList to xi.
	For simple mean calculation, this statement does nothing. For standard deviation, however, this statement computes the measure of deviation from the average.