Section 11.3
Stacks and Queues
A LINKED LIST is a particular type of
data structure, made up of objects linked together by pointers.
In the previous section, we used a linked list
to store an ordered list of Strings, and we implemented insert,
delete, and find operations on that list. However, we could
easily have stored the list of Strings in an array or ArrayList,
instead of in a linked list. We could still have implemented
insert, delete, and find operations on the list.
The implementations of these operations would have been different, but
their interfaces and logical behavior would still be the same.
The term abstract data type, or
ADT, refers to a set of possible values and
a set of operations on those values, without any specification of
how the values are to be represented or how the operations are to
be implemented. An "ordered list of strings" can be defined as an
abstract data type. Any sequence of Strings that is arranged
in increasing order is a possible value of this data type.
The operations on the data type include inserting a new string, deleting
a string, and finding a string in the list. There are often several different
ways to implement the same abstract data type. For example, the
"ordered list of strings" ADT can be implemented as a linked list or
as an array. A program that only depends on the abstract definition
of the ADT can use either implementation, interchangeably. In particular,
the implementation of the ADT can be changed without affecting the
program as a whole. This can make the program easier to debug and
maintain, so ADT's are an important tool in software engineering.
In this section, we'll look at two common abstract data types,
stacks and queues.
Both stacks and queues are often implemented as linked lists, but that
is not the only possible implementation. You should think of the rest of this
section partly as a discussion of stacks and queues and partly as
a case study in ADTs.
A stack consists of a sequence of items, which should be thought
of piled one on top of the other like a physical stack of boxes or
cafeteria trays. Only the top item on the stack is accessible
at any given time. It can be removed from the stack with an operation called
pop. An item lower down on the stack can
only be removed after all the items on top of it have been popped off the stack.
A new item can be added to the top of the stack with an operation called
push. We can make a stack of any type
of items. If, for example, the items are values of type int,
then the push and pop operations can be implemented as instance methods
void push (int newItem) -- Add newItem to top of stack.
int pop() -- Remove the top int from the stack and return it.
It is an error to try to pop an item from an empty stack, so it is
important to be able to tell whether a stack is empty. We need another
stack operation to do the test, implemented as an instance method
boolean isEmpty() -- Returns true if the stack is empty
This describes a "stack of ints" as an abstract data
type. This ADT can be implemented in several ways, but however it is
implemented, its behavior must correspond to the abstract mental image
of a stack.
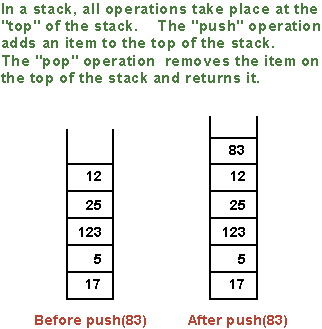
In the linked list implementation of a stack, the top of the
stack is actually the node at the head of the list. It is easy to
add and remove nodes at the front of a linked list -- much easier than
inserting and deleting nodes in the middle of the list. Here is a class
that implements the "stack of ints" ADT using a linked list.
(It uses a static nested class to represent the nodes of the linked
list. See Section 5.6 for a discussion of nested classes.
If the nesting bothers you, you could replace it with a separate Node
class.)
public class StackOfInts {
private static class Node {
// An object of type Node holds one of the
// items in the linked list that represents the stack.
int item;
Node next;
}
private Node top; // Pointer to the Node that is at the top of
// of the stack. If top == null, then the
// stack is empty.
public void push( int N ) {
// Add N to the top of the stack.
Node newTop; // A Node to hold the new item.
newTop = new Node();
newTop.item = N; // Store N in the new Node.
newTop.next = top; // The new Node points to the old top.
top = newTop; // The new item is now on top.
}
public int pop() {
// Remove the top item from the stack, and return it.
// Note that this routine will throw a NullPointerException
// if an attempt is made to pop an item from an empty
// stack. (It would be better style to define a new
// type of Exception to throw in this case.)
int topItem = top.item; // The item that is being popped.
top = top.next; // The previous second item is now on top.
return topItem;
}
public boolean isEmpty() {
// Returns true if the stack is empty. Returns false
// if there are one or more items on the stack.
return (top == null);
}
} // end class StackOfInts
You should make sure that you understand how the push and pop
operations operate on the linked list. Drawing some pictures might help.
Note that the linked list is part of the private implementation of
the StackOfInts class. A program that uses this class doesn't
even need to know that a linked list is being used.
Now, it's pretty easy to implement a stack as an array instead of as
a linked list. Since the number of items on the stack varies with
time, a counter is needed to keep track of how many spaces in the
array are actually in use. If this counter is called top,
then the items on the stack are stored in positions 0, 1, ..., top-1
in the array. The item in position 0 is on the bottom of the
stack, and the item in position top-1 is on the top of the stack.
Pushing an item onto the stack is easy: Put the item in position
top and add 1 to the value of top. If we
don't want to put a limit on the number of items that the stack can
hold, we can use the dynamic array techniques from Section 8.3.
Note that the typical picture of the array would show the stack "upside down",
with the top of the stack at the bottom of the array. This doesn't
matter. The array is just an implementation of the abstract idea of a
stack, and as long as the stack operations work the way they are supposed
to, we are OK. Here is a second implementation of the StackOfInts
class, using a dynamic array:
public class StackOfInts {
private int[] items = new int[10]; // Holds the items on the stack.
private int top = 0; // The number of items currently on the stack.
public void push( int N ) {
// Add N to the top of the stack.
if (top == items.length) {
// The array is full, so make a new, larger array and
// copy the current stack items into it.
int[] newArray = new int[ 2*items.length ];
System.arraycopy(items, 0, newArray, 0, items.length);
items = newArray;
}
items[top] = N; // Put N in next available spot.
top++; // Number of items goes up by one.
}
public int pop() {
// Remove the top item from the stack, and return it.
// Note that this routine will throw an
// ArrayIndexOutOfBoundsException if an attempt is
// made to pop an item from an empty stack.
// (It would be better style to define a new
// type of Exception to throw in this case.)
int topItem = items[top - 1] // Top item in the stack.
top--; // Number of items on the stack goes down by one.
return topItem;
}
public boolean isEmpty() {
// Returns true if the stack is empty. Returns false
// if there are one or more items on the stack.
return (top == 0);
}
} // end class StackOfInts
Once again, the implentation of the stack (as an array) is private to
the class. The two versions of the StackOfInts class can be used
interchangeably. If a program uses one version, it should be possible
to substitute the other version without changing the program. Unfortunately,
though, there is one detail in which the classes behave differently: When
an attempt is made to pop an item from an empty stack, the first version
of the class will generate a NullPointerException while the
second will generate an ArrayIndexOutOfBoundsException. It
would be better to define a new EmptyStackException class
and use it in both versions. In fact, the original description of
the "stack of ints" ADT should have specified exactly what happens when an
attempt is made to pop an item from an empty stack. This is just the
sort of small detail that is often left out of interface specifications,
causing no end of problems!
Queues are similar to stacks in that a queue consists of a sequence of
items, and there are restrictions about how items can be added to and
removed from the list. However, a queue has two ends, called the
front and the back of the queue. Items are always added to the
queue at the back and removed from the queue at the front. The operations
of adding and removing items are called enqueue
and dequeue. An item that
is added to the back of the queue will remain on the queue until all the
items in front of it have been removed. This should sound familiar.
A queue is like a "line" or "queue" of customers waiting for service.
Customers are serviced in the order in which they arrive on the queue.
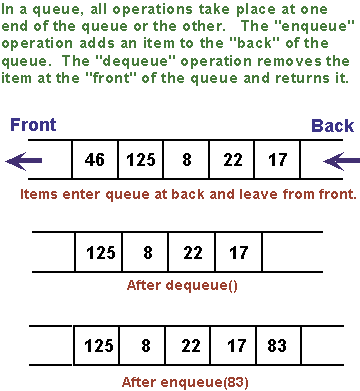
A queue can hold items of any type. For a queue of ints, the
enqueue and dequeue operations can be implemented as instance methods in
a "QueueOfInts" class.
We also need an instance method for checking whether the queue is empty:
void enqueue(int N) -- Add N to the back of the queue.
int dequeue() -- Remove the item at the front and return it.
boolean isEmpty() -- Return true if the queue is empty.
A queue can be implemented as a linked list or as an array. An
efficient array implementation is a little trickier than the array
implementation of a stack, so I won't give it here. In the linked
list implementation, the first item of the list is the front
of the queue. Dequeueing an item from the front of the queue is
just like popping an item off a stack. The back of the queue is
at the end of the list. Enqueueing an item involves setting a pointer
in the last node on the current list to point to a new node that contains
the item. To do this, we'll need a command like "tail.next = newNode;",
where tail is a pointer to the last node in the list. If
head is a pointer to the first node of the list, it would
always be possible to get a pointer to the last node of the list
by saying:
Node tail; // This will point to the last node in the list.
tail = head; // Start at the first node.
while (tail.next != null) {
tail = tail.next;
}
// At this point, tail.next is null, so tail points to
// the last node in the list.
However, it would be very inefficient to do this over and over
every time an item is enqueued. For the sake of efficiency, we'll
keep a pointer to the last node in an instance
variable. We just have to be careful to
update the value of this variable whenever a new node is added
to the end of the list. Given all this, writing the QueueOfInts
class is not very difficult:
public class QueueOfInts {
private static class Node {
// An object of type Node holds one of the items
// in the linked list that represents the queue.
int item;
Node next;
}
private Node head = null; // Points to first Node in the queue.
// The queue is empty when head is null.
private Node tail = null; // Points to last Node in the queue.
void enqueue( int N ) {
// Add N to the back of the queue.
Node newTail = new Node(); // A Node to hold the new item.
newTail.item = N;
if (head == null) {
// The queue was empty. The new Node becomes
// the only node in the list. Since it is both
// the first and last node, both head and tail
// point to it.
head = newTail;
tail = newTail;
}
else {
// The new node becomes the new tail of the list.
// (The head of the list is unaffected.)
tail.next = newTail;
tail = newTail;
}
}
int dequeue() {
// Remove and return the front item in the queue.
// Note that this can throw a NullPointerException.
int firstItem = head.item;
head = head.next; // The previous second item is now first.
if (head == null) {
// The queue has become empty. The Node that was
// deleted was the tail as well as the head of the
// list, so now there is no tail. (Actually, the
// class would work fine without this step.)
tail = null;
}
return firstItem;
}
boolean isEmpty() {
// Return true if the queue is empty.
return (head == null);
}
} // end class QueueOfInts
Queues are typically used in a computer (as in real life) when
only one item can be processed at a time, but several items can
be waiting for processing. For example:
- In a Java program that
has multiple threads, the threads that want processing time on the CPU
are kept in a queue. When a new thread is started, it is added to the
back of the queue. A thread is removed from the front of the queue,
given some processing time, and then -- if it has not terminated --
is sent to the back of the queue to wait for another turn.
- Events such as keystrokes and mouse clicks are stored in a queue
called the "event queue". A program removes events from the event
queue and processes them. It's possible for several more events to
occur while one event is being processed, but since the events are
stored in a queue, they will always be processed in the order in
which they occurred.
- A ServerSocket, as covered in Section 10.4,
has an associated queue which contains connection requests that have
been received but not yet serviced. The ServerSocket's
accept() method gets the next connection request from the
front of this queue.
Queues are said to implement a FIFO
policy: First In, First Out. Or, as it is more commonly expressed,
first come, first served. Stacks, on the other hand implement a
LIFO policy: Last In, First Out.
The item that comes out of the stack is the last one that was put in.
Just like queues, stacks can be used to hold items that are waiting
for processing (although in applications where queues are typically
used, a stack would be considered "unfair").
To get a better handle on the difference between stacks and queues,
consider the applet shown below. When you click on a white square in
the grid, the applet will gradually mark all the squares in the
grid, starting from the one where you click. To understand how
the applet does this, think of yourself in the place of the applet.
When the user clicks a square, you are handed an index card.
The location of the square -- its row and column -- is written on the card.
You put the card in a pile, which then contains just that one card.
Then, you repeat the following:
If the pile is empty, you are done. Otherwise, take an index card
from the pile. The index card specifies a square. Look at each
horizontal and vertical neighbor of that square. If the neighbor
has not already been encountered, write its location on an index
card and put the card in the pile.
While a square is in the pile, waiting to be processed, it is
colored red. When a square is taken from the pile and processed,
its color changes to gray. Eventually, all the squares have been processed
and the procedure ends. In the index card analogy, the pile
of cards contains all the red squares.
The applet can use your choice of three methods: Stack, Queue,
and Random. In each case, the same general procedure is used. The
only difference is how the "pile of index cards" is managed. For a
stack, cards are added and removed at the top of the pile. For
a queue, cards are added to the bottom of the pile and removed from
the top. In the random case, the card to be processed is picked
at random from among the cards in the pile. The order of processing
is very different in these three cases.
You should experiment with the applet to see how it all works.
Try to understand how stacks and queues are being used. Try starting
from one of the corner squares. While the process is going on,
you can click on other white squares, and they will be added to
the pile. When you do this with a stack, you should notice that
the square you click is processed immediately, and all the red squares
that were already waiting for processing have to wait. On the other
hand, if you do this with a queue, the square that you click will
wait its turn. The source code for this applet can be found in
the file DepthBreadth.java.
Queues seem very natural because they occur so often in real life,
but there are times when stacks are appropriate and even essential.
For example, consider what happens when a routine calls a subroutine.
The first routine is suspended while the subroutine is executed,
and it will continue only when the subroutine returns. Now, suppose
that the subroutine calls a second subroutine, and the second subroutine
calls a third, and so on. Each subroutine is suspended while the
subsequent subroutines are executed. The computer has to keep track
of all the subroutines that are suspended. It does this with a stack.
When a subroutine is called, an activation
record is created for that subroutine. The activation record
contains information relevant to the execution of the subroutine,
such as its local variables and parameters. The activation record
for the subroutine is placed on a stack. It will be removed from
the stack and destroyed when the subroutine returns. If the subroutine
calls another subroutine, the activation record of the second subroutine
is pushed onto the stack, on top of the activation record of the first
subroutine. The stack can continue to grow as more subroutines are
called, and it shrinks as those subroutines return.
As another example, stacks can be used to evaluate postfix
expressions. An ordinary mathematical expression such as
2+(15-12)*17 is called an infix expression.
In an infix expression, an operator comes in between its two operands,
as in "2 + 2". In a postfix expression, an operator comes
after its two operands, as in "2 2 +". The infix expression
"2+(15-12)*17" would be written in postfix form as
"2 15 12 - 17 * +". The
"-" operator in this expression applies to the two operands that
precede it, namely "15" and "12". The "*" operator applies to the two
operands that precede it, namely "15 12 -" and
"17". And the "+" operator applies to "2" and
"15 12 - 17 *". These are the same
computations that are done in the original infix expression.
Now, suppose that we want to process the expression
"2 15 12 - 17 * +", from left to right,
and find its value. The first item we encounter is the 2, but what can
we do with it? At this point, we don't know what operator, if any, will be applied
to the 2 or what the other operand might be. We have to remember the
2 for later processing. We do this by pushing it onto a stack.
Moving on to the next item, we see a 15, which is pushed onto the stack
on top of the 2. Then the 12 is added to the stack.
Now, we come to the operator, "-". This operation applies to the two operands
that preceded it in the expression. We have saved those two operands on the
stack. So, to process the "-" operator, we pop two numbers from the stack, 12
and 15, and compute 15 - 12 to get the answer 3.
This 3 will be used for later processing, so we push it onto the stack,
on top of the 2, which is still waiting there. The next item in the expression
is a 17, which is processed by pushing it onto the stack, on top of the
3. To process the next item, "*", we pop two numbers from the
stack. The numbers are 17 and the 3 that represents the
value of "15 12 -". These numbers are multiplied, and the result, 51
is pushed onto the stack. The next item in the expression is a "+" operator, which
is processed by popping 51 and 2 from the stack, adding them, and pushing the
result, 53, onto the stack. Finally, we've come to the end of the
expression. The number on the stack is the value of the entire expression,
so all we have to do is pop the answer from the stack, and we are done!
The value of the expression is 53.
Although it's easier for people to work with infix expressions, postfix
expressions have some advantages. For one thing, postfix expressions don't
require parentheses or precedence rules. The order in which operators are
applied is determined entirely by the order in which they occur in the expression.
This allows the algorithm for evaluating postfix expressions to be fairly straightforward:
Start with an empty stack
for each item in the expression:
if the item is a number:
Push the number onto the stack
else if the item is an operator:
Pop the operands from the stack // Can generate an error
Apply the operator to the operands
Push the result onto the stack
else
There is an error in the expression
Pop a number from the stack
if the stack is not empty:
There is an error in the expression
else:
The last number that was popped is the value of the expression
Errors in an expression can be detected easily. For example,
in the expression "2 3 + *", there are not enough operands
for the "*" operation. This will be detected in the algorithm when
an attempt is made to pop the second operand for "*" from the stack,
since the stack will be empty. The opposite problem occurs in
"2 3 4 +". There are not enough operators for all the
numbers. This will be detected when the 2 is left still sitting in the
stack at the end of the algorithm.
This algorithm is demonstrated in the sample
program PostfixEval.java,
which lets you type in postfix expressions made up of non-negative real numbers and the
operators "+", "-", "*", "/", and "^". The "^"
represents exponentiation. That is, "2 3 ^" is evaluated
as 23. The program prints out a message as it processes each
item in the expression. The stack class used in the program is defined in the file
NumberStack.java. The NumberStack
class is identical to the first StackOfInts class, given above, except
that it has been modified to store values of type double instead of
values of type int.
Here is an applet that simulates the PostfixEval program:
The only interesting aspect of this program is the method that
implements the postfix evaluation algorithm. It is a direct
implementation of the pseudocode algorithm given above:
static void readAndEvaluate() {
// Read one line of input and process it as a postfix expression.
// If the input is not a legal postfix expression, then an error
// message is displayed. Otherwise, the value of the expression
// is displayed. It is assumed that the first character on
// the input line is a non-blank. (This is checked in the
// main() routine.)
NumberStack stack; // For evaluating the expression.
stack = new NumberStack(); // Make a new, empty stack.
TextIO.putln();
while (TextIO.peek() != '\n') {
if ( Character.isDigit(TextIO.peek()) ) {
// The next item in input is a number. Read it and
// save it on the stack.
double num = TextIO.getDouble();
stack.push(num);
TextIO.putln(" Pushed constant " + num);
}
else {
// Since the next item is not a number, the only thing
// it can legally be is an operator. Get the operator
// and perform the operation.
char op; // The operator, which must be +, -, *, /, or ^.
double x,y; // The operands, from the stack.
double answer; // The result, to be pushed onto the stack.
op = TextIO.getChar();
if (op != '+' && op != '-' && op != '*'
&& op != '/' && op != '^') {
// The character is not one of the legal operations.
TextIO.putln("\nIllegal operator found in input: " + op);
return;
}
if (stack.isEmpty()) {
TextIO.putln(
" Stack is empty while trying to evaluate " + op);
TextIO.putln("\nNot enough numbers in expression!");
return;
}
y = stack.pop();
if (stack.isEmpty()) {
TextIO.putln(
" Stack is empty while trying to evaluate " + op);
TextIO.putln("\nNot enough numbers in expression!");
return;
}
x = stack.pop();
switch (op) {
case '+': answer = x + y; break;
case '-': answer = x - y; break;
case '*': answer = x * y; break;
case '/': answer = x / y; break;
default: answer = Math.pow(x,y); // (op must be '^'.)
}
stack.push(answer);
TextIO.putln(" Evaluated " + op + " and pushed " + answer);
}
skipSpaces(); // Skips past any blanks in the intput, before
// going back to the start of the while loop to
// test TextIO.peek() again.
} // end while
// If we get to this point, the input has been read successfully.
// If the expression was legal, then the value of the expression is
// on the stack, and it is the only thing on the stack.
if (stack.isEmpty()) { // Impossible if input is really non-empty.
TextIO.putln("No expression provided.");
return;
}
double value = stack.pop(); // Value of the expression.
TextIO.putln(" Popped " + value + " at end of expression.");
if (stack.isEmpty() == false) {
TextIO.putln(" Stack is not empty.");
TextIO.putln("\nNot enough operators for all the numbers!");
return;
}
TextIO.putln("\nValue = " + value);
} // end readAndEvaluate()
Postfix expressions are often used internally by computers. In fact, the
Java virtual machine is a "stack machine" which uses the stack-based approach to
expression evaluation that we have been discussing. The algorithm can easily
be extended to handle variables, as well as constants. When a variable is
encountered in the expression, the value of the variable is pushed onto the
stack. It also works for operators with more or fewer than two operands.
As many operands as are needed are popped from the stack and the result is
pushed back on to the stack. For example, the unary
minus operator, which is used in the expression "-x",
has a single operand. We will continue to look at expressions and expression
evaluation in the next two sections.
