| Thinking in C++ Vol 2 - Practical Programming |
|
Prev |
Home |
Next |
So what was meant to be a convenient way to perform type
parameter substitution turned out to be a mechanism to support compile-time
programming. Such a program is called a template metaprogram
(since you re in effect programming a program ), and it turns out that you can
do quite a lot with it. In fact, template metaprogramming is Turing complete because it supports selection (if-else) and looping (through recursion). Theoretically,
then, you can perform any computation with it. The
factorial example above shows how to implement repetition: write a recursive
template and provide a stopping criterion via a specialization. The following
example shows how to compute Fibonacci numbers at compile time by the same
technique:
//: C05:Fibonacci.cpp
#include <iostream>
using namespace std;
template<int n> struct Fib {
enum { val = Fib<n-1>::val +
Fib<n-2>::val };
};
template<> struct Fib<1> { enum { val = 1 };
};
template<> struct
Fib<0> { enum { val = 0 }; };
int main() {
cout << Fib<5>::val << endl; // 6
cout << Fib<20>::val << endl; //
6765
} ///:~
Fibonacci numbers are defined mathematically as:
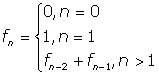
The first two cases lead to the template specializations
above, and the rule in the third line becomes the primary template.
Compile time looping
To compute any loop in a template metaprogram, it must first
be reformulated recursively. For example, to raise the integer n to the
power p, instead of using a loop such as in the following lines:
int val = 1;
while(p--)
val *=
n;
you cast it as a recursive procedure:
int power(int n, int p) {
return (p == 0) ? 1 : n*power(n, p - 1);
}
This can now be easily rendered as a template metaprogram:
//: C05:Power.cpp
#include <iostream>
using namespace std;
template<int N, int P> struct Power {
enum { val = N * Power<N, P-1>::val };
};
template<int N> struct Power<N, 0> {
enum { val = 1 };
};
int main() {
cout << Power<2, 5>::val << endl;
// 32
} ///:~
We need to use a partial specialization for the stopping
condition, since the value N is still a free template parameter. Note
that this program only works for non-negative powers.
The following metaprogram adapted from Czarnecki and Eisenecker is interesting
in that it uses a template template parameter, and simulates passing a function
as a parameter to another function, which loops through the numbers 0..n:
//: C05:Accumulate.cpp
// Passes a "function" as a parameter at
compile time.
#include <iostream>
using namespace std;
// Accumulates the results of F(0)..F(n)
template<int n, template<int> class F> struct
Accumulate {
enum { val = Accumulate<n-1, F>::val +
F<n>::val };
};
// The stopping criterion (returns the value F(0))
template<template<int> class F> struct
Accumulate<0, F> {
enum { val = F<0>::val };
};
// Various "functions":
template<int n> struct
Identity {
enum { val = n };
};
template<int n> struct Square {
enum { val = n*n };
};
template<int n> struct Cube {
enum { val = n*n*n };
};
int main() {
cout << Accumulate<4, Identity>::val
<< endl; // 10
cout << Accumulate<4, Square>::val
<< endl; // 30
cout << Accumulate<4, Cube>::val <<
endl; // 100
} ///:~
The primary Accumulate template attempts to compute
the sum F(n)+F(n‑1) F(0). The stopping criterion is obtained by a
partial specialization, which returns F(0). The parameter F is
itself a template, and acts like a function as in the previous examples in this
section. The templates Identity, Square, and Cube compute
the corresponding functions of their template parameter that their names
suggest. The first instantiation of Accumulate in main( )
computes the sum 4+3+2+1+0, because the Identity function simply
returns its template parameter. The second line in main( ) adds
the squares of those numbers (16+9+4+1+0), and the last computes the sum of the
cubes (64+27+8+1+0).
Loop unrolling
Algorithm designers have always endeavored to optimize their
programs. One time-honored optimization, especially for numeric programming, is
loop unrolling, a technique that minimizes loop overhead. The quintessential
loop-unrolling example is matrix multiplication. The following function
multiplies a matrix and a vector. (Assume that the constants ROWS and COLS
have been previously defined.):
void mult(int a[ROWS][COLS], int x[COLS], int y[COLS])
{
for(int i = 0; i < ROWS; ++i) {
y[i] = 0;
for(int j = 0; j < COLS; ++j)
y[i] += a[i][j]*x[j];
}
}
If COLS is an even number, the overhead of
incrementing and comparing the loop control variable j can be cut in
half by unrolling the computation into pairs in the inner loop:
void mult(int a[ROWS][COLS], int x[COLS], int y[COLS])
{
for(int i = 0; i < ROWS; ++i) {
y[i] = 0;
for(int j = 0; j < COLS; j += 2)
y[i] += a[i][j]*x[j] + a[i][j+1]*x[j+1];
}
}
In general, if COLS is a factor of k, k
operations can be performed each time the inner loop iterates, greatly reducing
the overhead. The savings is only noticeable on large arrays, but that is
precisely the case with industrial-strength mathematical computations.
Function inlining also constitutes a form of loop unrolling.
Consider the following approach to computing powers of integers:
//: C05:Unroll.cpp
// Unrolls an implicit loop via inlining.
#include <iostream>
using namespace std;
template<int n> inline int power(int m) {
return power<n-1>(m) * m;
}
template<> inline int power<1>(int m) {
return m;
}
template<> inline int power<0>(int m) {
return 1;
}
int main() {
int m = 4;
cout << power<3>(m) << endl;
} ///:~
Conceptually, the compiler must generate three
specializations of power<>, one each for the template parameters
3, 2, and 1. Because the code for each of these functions can be inlined, the
actual code that is inserted into main( ) is the single expression m*m*m.
Thus, a simple template specialization coupled with inlining provides a way to
totally avoid loop control overhead. This
approach to loop unrolling is limited by your compiler s inlining depth.
Compile time selection
To simulate conditionals at compile time, you can use the
conditional ternary operator in an enum declaration. The following
program uses this technique to calculate the maximum of two integers at compile
time:
//: C05:Max.cpp
#include <iostream>
using namespace std;
template<int n1, int n2> struct Max {
enum { val = n1 > n2 ? n1 : n2 };
};
int main() {
cout << Max<10, 20>::val << endl;
// 20
} ///:~
If you want to use compile-time conditions to govern custom
code generation, you can use specializations of the values true and false:
//: C05:Conditionals.cpp
// Uses compile-time conditions to choose code.
#include <iostream>
using namespace std;
template<bool cond> struct Select {};
template<> class Select<true> {
static void statement1() {
cout << "This is statement1 executing\n";
}
public:
static void f() { statement1(); }
};
template<> class Select<false> {
static void statement2() {
cout << "This is statement2
executing\n";
}
public:
static void f() { statement2(); }
};
template<bool cond> void execute() {
Select<cond>::f();
}
int main() {
execute<sizeof(int) == 4>();
} ///:~
This program is equivalent to the expression:
if(cond)
statement1();
else
statement2();
except that the condition cond is evaluated at
compile time, and the appropriate versions of execute<>( ) and
Select<> are instantiated by the compiler. The function Select<>::f( )
executes at runtime. A switch statement can be emulated in similar
fashion, but specializing on each case value instead of the values true
and false.
Compile time assertions
In Chapter 2 we touted the virtues of using assertions as
part of an overall defensive programming strategy. An assertion is basically an
evaluation of a Boolean expression followed by a suitable action: do nothing if
the condition is true, or halt with a diagnostic message otherwise. It s best to
discover assertion failures as soon as possible. If you can evaluate an
expression at compile time, use a compile-time assertion. The following example
uses a technique that maps a Boolean expression to an array declaration:
//: C05:StaticAssert1.cpp {-xo}
// A simple, compile-time assertion facility
#define STATIC_ASSERT(x) \
do { typedef int a[(x) ? 1 : -1]; } while(0)
int main() {
STATIC_ASSERT(sizeof(int) <= sizeof(long)); //
Passes
STATIC_ASSERT(sizeof(double) <= sizeof(int)); //
Fails
} ///:~
The do loop creates a temporary scope for the
definition of an array, a, whose size is determined by the condition in
question. It is illegal to define an array of size -1, so when the condition is
false the statement should fail.
The previous section showed how to evaluate compile-time Boolean
expressions. The remaining challenge in emulating assertions at compile time is
to print a meaningful error message and halt. All that is required to halt the
compiler is a compile error; the trick is to insert helpful text in the error
message. The following example from Alexandrescu uses template
specialization, a local class, and a little macro magic to do the job:
//: C05:StaticAssert2.cpp {-g++}
#include <iostream>
using namespace std;
// A template and a specialization
template<bool> struct StaticCheck {
StaticCheck(...);
};
template<> struct StaticCheck<false> {};
// The macro (generates a local class)
#define STATIC_CHECK(expr, msg) { \
class Error_##msg {}; \
sizeof((StaticCheck<expr>(Error_##msg()))); \
}
// Detects narrowing conversions
template<class To, class From> To safe_cast(From
from) {
STATIC_CHECK(sizeof(From) <= sizeof(To),
NarrowingConversion);
return reinterpret_cast<To>(from);
}
int main() {
void* p = 0;
int i = safe_cast<int>(p);
cout << "int cast okay << endl;
//! char c = safe_cast<char>(p);
} ///:~
This example defines a function template, safe_cast<>( ),
that checks to see if the object it is casting from is no larger than the type
of object it casts to. If the size of the target object type is smaller, then
the user will be notified at compile time that a narrowing conversion was
attempted. Notice that the StaticCheck class template has the curious
feature that anything can be converted to an instance of StaticCheck<true>
(because of the ellipsis in its constructor),
and nothing can be converted to a StaticCheck<false>
because no conversions are supplied for that specialization. The idea is to
attempt to create an instance of a new class and attempt to convert it to StaticCheck<true>
at compile time whenever the condition of interest is true, or to a StaticCheck<false>
object when the condition being tested is false. Since the sizeof
operator does its work at compile time, it is used to attempt the conversion.
If the condition is false, the compiler will complain that it doesn t know how
to convert from the new class type to StaticCheck<false>. (The
extra parentheses inside the sizeof invocation in STATIC_CHECK( )
are to prevent the compiler from thinking that we re trying to invoke sizeof
on a function, which is illegal.) To get some meaningful information inserted
into the error message, the new class name carries key text in its name.
The best way to understand this technique is to walk through
a specific case. Consider the line in main( ) above which reads:
int i =
safe_cast<int>(p);
The call to safe_cast<int>(p) contains the
following macro expansion replacing its first line of code:
{ \
class Error_NarrowingConversion {}; \
sizeof(StaticCheck<sizeof(void*) <= sizeof(int)>
\
(Error_NarrowingConversion())); \
}
(Recall that the token-pasting preprocessing operator, ##,
concatenates its operand into a single token, so Error_##NarrowingConversion
becomes the token Error_NarrowingConversion after preprocessing). The
class Error_NarrowingConversion is a local class (meaning that it
is declared inside a non-namespace scope) because it is not needed elsewhere in
the program. The application of the sizeof operator here attempts to
determine the size of an instance of StaticCheck<true> (because sizeof(void*)
<= sizeof(int) is true on our platforms), created implicitly from the
temporary object returned by the call Error_NarrowingConversion( ).
The compiler knows the size of the new class Error_NarrowingConversion (it s
empty), and so the compile-time use of sizeof at the outer level in STATIC_CHECK( )
is valid. Since the conversion from the Error_NarrowingConversion
temporary to StaticCheck<true> succeeds, so does this outer
application of sizeof, and execution continues.
Now consider what would happen if the comment were removed
from the last line of main( ):
char c
= safe_cast<char>(p);
Here the STATIC_CHECK( ) macro inside safe_cast<char>(p)
expands to:
{ \
class Error_NarrowingConversion {}; \
sizeof(StaticCheck<sizeof(void*) <=
sizeof(char)> \
(Error_NarrowingConversion())); \
}
Since the expression sizeof(void*) <= sizeof(char)
is false, a conversion from an Error_NarrowingConversion temporary to StaticCheck<false>
is attempted, as follows:
sizeof(StaticCheck<false>(Error_NarrowingConversion()));
which fails, so the compiler halts with a message something
like the following:
Cannot cast from
'Error_NarrowingConversion' to 'StaticCheck<0>' in function
char safe_cast<char,void *>(void *)
The class name Error_NarrowingConversion is the
meaningful message judiciously arranged by the coder. In general, to perform a
static assertion with this technique, you just invoke the STATIC_CHECK
macro with the compile-time condition to check and with a meaningful name to
describe the error.
| Thinking in C++ Vol 2 - Practical Programming |
|
Prev |
Home |
Next |
