From Robert Banks, Slicing Pizzas, Racing Turtles, and Further Adventures in Applied Mathematics [Banks02].

This project is simple: it does not use loops, if-statements or any data structures. This exercise focuses on expressions and assignment statements.

Facts about the American flag. The standard dimension is the width (or hoist). This is the basic unit that all others are multiplied by. A flag that is 30 inches wide will simply have 30 inches multiplied by all of the other measurements.

These are other facts; they are counts, not measurements.

Red Area. There are 4 red stripes which abut the blue field and 3 red stripes run the full length of the flag.

We can compute the area of the red, since it is 4 short rectangles and 3 long rectangles. The short rectangle areas are the width of a stripe (Ws) times the whole length (length of the fly, Lf) less the width of the blue union (Wu). The long rectangle areas are simply the width of the stripe (Ws) times the length of the fly (Lf).

Red = 4×Ws×(Lf-Lu) + 3×Ws×(Lf).

White Area. There are 3 white stripes which abut the blue field, 3 whie stripes run the full length of the flag, plus there are the 50 stars.

We can compute the basic area of the white using a similar analysis as area of the red, and adding in the areas of the stars, 50 S . We'll return to the area of the stars, 50 S , last.

White = 3×Ws×(Lf-Lu) + 3×Ws×(Lf) + 50S.

Blue Area. The blue area is the area of the union, less the area of the stars, 50 S .

Blue = (Lu-Wu) - 50S.

Area of the Stars. A 5-sided star (pentagram) can be analyzed as 5 kites of 2 triangles. The area of each kite, K , is computed as follows.

The inner angles of all five kites fill the inside of the pentagram, and the angles must sum to 360°, therefore each inner angle is 72°. Angles of a triangle sum to 180°, therefore the lower triangle has two side angles of (180°-72°)/2 = 54°.

We see some straight lines that contain an outer triangle and two inner triangles. We know the inner triangles add to 108°, a straight line is 180° so the outer triangle has two 72° corners and a 36° peak. The area of the two triangles can be computed as

a=36°, b=72°

Note that the math library sin and cos functions operate in radians, not degrees. The conversion rule is π radians = 180 degrees. Therefore, we often see something like sin ( a ×π/180 ) to convert a degrees to radians.

The Golden Ratio is 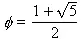(about 1.61803).

The total area of a star is

S=5×K.

Given a specific width of a flag (in feet), we can compute the actual areas of each color.

Check Your Results. Blue is 18.73% of the total area.